Understanding Slew Rate in Op-Amp
by jobitjoseph in Circuits > Electronics
919 Views, 0 Favorites, 0 Comments
Understanding Slew Rate in Op-Amp

An ideal op-amp is a voltage amplifier with infinite input impedance, zero output impedance, and infinite bandwidth. In the real world, however, these parameters are limited by small imperfections in semiconductor manufacturing, effects of temperature, and so on. There is one parameter that is much overlooked but stands out in the above regard, and that is the slew rate. It is not a parasitic effect, but rather a deliberate slowing down of the op-amp to ensure stability.
In this article, we will learn about the slew rate of an operational amplifier, and where it comes from, and we will also do some calculations for the classic 741 op-amp.
What Is Slew Rate?

The slew Rate is defined as the maximum rate of change of an opamp’s output voltage. In other words, Slew rate basically refers to how fast the op-amp is capable of changing its output voltage in response to a change in input. The slew rate is usually measured in units of a volt per unit of time, more commonly in volts per microsecond, or V/µs.
Unit of Slew Rate = V/uS
An ideal op-amp has an infinite slew rate, meaning it can change its output instantly with any change in input. It is usually measured by giving a step signal to the input of the opamp and measuring the rate of change from 10% to 90% of the output signal’s amplitude.
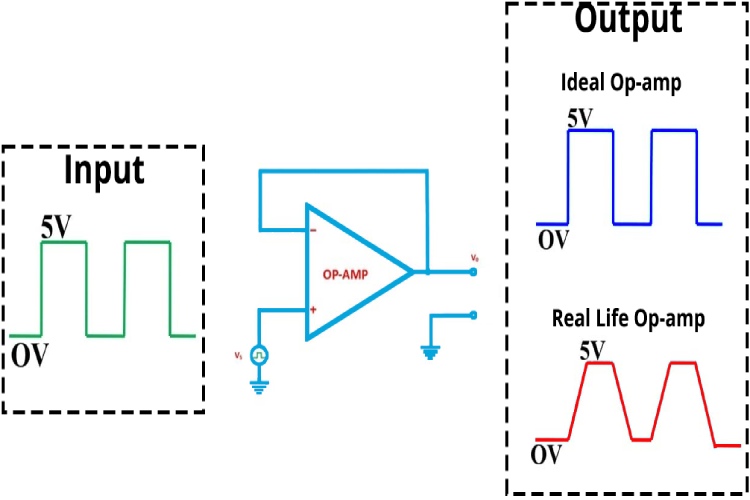
To understand it more easily let's look at an example. In the above image, you can see that we have configured an op-amp as a voltage follower. Ideally, the output should follow the input signal. On the input side of the voltage follower, we are applying a square wave signal, which is marked in green colour. Ideally, the output should have the same waveform without any distortions, which is displayed as the blue-coloured waveform. But in reality, that's not the case. Output won’t be the same as the input because of the slew rate and many other factors. The waveform in the red colour is a representation of the output, due to the slew rate.
The diagram given below shows the output of an op-amp in response to a step input.
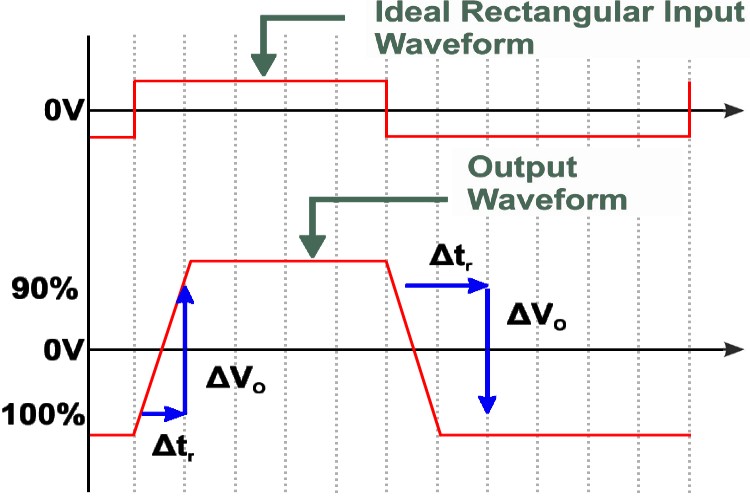
As we can see in the diagram, the output voltage does not rise immediately following the input. The op-amp has a finite rise time, where the voltage increases linearly with time. This slope of the output voltage with respect to time is the slew rate
Check this out to know why Op-Amps Slew Rate Limited.
Impact of Input Signal Characteristics on Slew Rate
While the inherent slew rate of an op-amp is determined by its internal design, the characteristics of the input signal can also influence how the slew rate affects circuit performance. Understanding these influences is essential for designing effective circuits that operate within the desired specifications. Here, we explore various input signal parameters and how they can impact the effective slew rate in a circuit.
- Amplitude of the Input Signal: The amplitude of the input signal plays a significant role in determining the demand on the op-amp's slew rate. A larger voltage swing requires the output to change more rapidly, which means the op-amp must have a sufficiently high slew rate to accommodate this change without distorting the signal. If the input signal demands a rate of change faster than the op-amp can provide, the output will exhibit a slower transition than the input, leading to waveform distortion, particularly in high-frequency or large-signal applications.
- Frequency of the Input Signal: The frequency of the input signal is directly related to how quickly the output needs to respond. High-frequency signals require the output voltage to change rapidly, increasing the demand on the slew rate. For sine waves, the slew rate requirement is calculated as SR 2fVPeak, Where f is the frequency and VPeakis the peak voltage of the signal. If the op-amp’s slew rate is lower than what the frequency and amplitude of the input signal require, it will result in a distorted output where the signal is unable to follow the input waveform accurately, particularly at the peaks of the waveforms.
- Rise and Fall Times of the Input Signal: The rise and fall times of an input signal, which are particularly relevant for digital signals like square waves, determine how quickly the signal transitions from one level to another. Op-amps with insufficient slew rates will struggle to replicate sharp transitions, leading to rounded edges in the output signal. This effect can degrade the performance of digital circuits, where precise timing is critical, and can also introduce timing errors, signal integrity issues, or even data loss in high-speed communication applications.
Frequency Compensation and Slew Rate
The output swing is deliberately limited in op-amps to ensure stability through the use of a compensation capacitor, which provides frequency compensation and limits the output slew rate. The figure given below shows the effects of having frequency compensation in an op-amp.
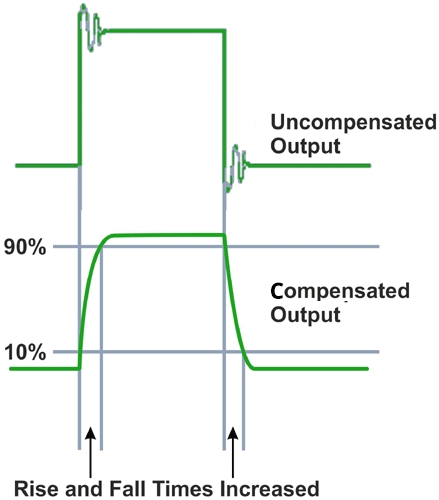
Although uncompensated op-amps are faster, because of the fast-rising and falling edges, there is ringing present, and this can lead to stability issues. To avoid this, compensation is implemented by adding a Miller capacitor to the driver stage of the op-amp.
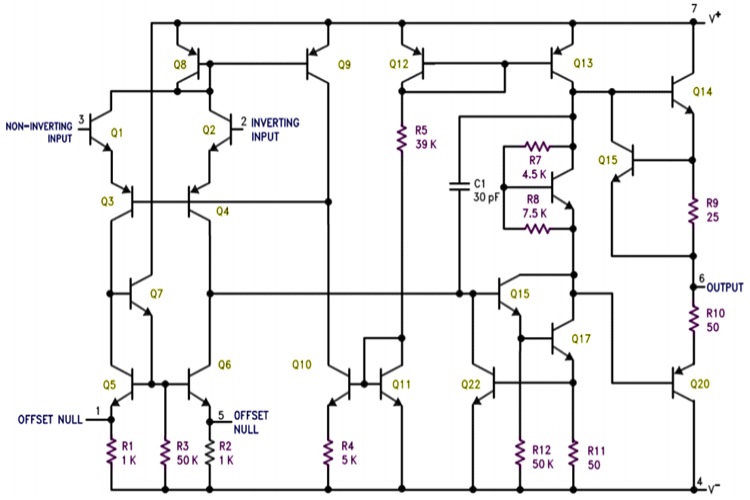
In the above figure, which shows the internal schematics of a typical op-amp, the compensation capacitor is C1, with a small value of 30pF. It is placed between the input and output of the output transistor driver. This can be simplified in the below figure.
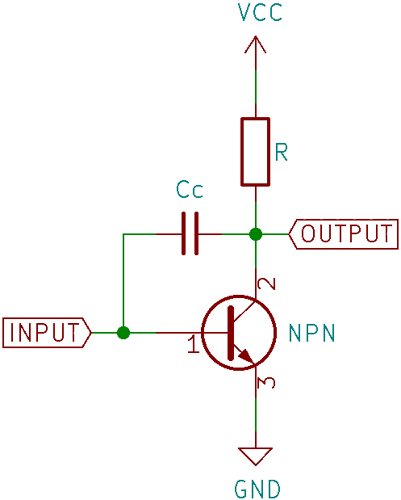
Here, a capacitor is added between the base and the collector. This capacitor is sometimes referred to as a Miller capacitor because it is similar to the parasitic Miller capacitance between the base and collector of a BJT transistor. As the input rises, the output on the collector begins to fall. This creates a voltage difference across the capacitor, and a current begins to flow through it.
Following the simple formula that relates voltage, current, capacitance, and time for a capacitor:
ic= C x dv/dt
where ic is the capacitor current, C is Capacitance and dv/dt is the rate of change of voltage.
From this, we can get that
slew rate dv/dt = ic/C.
We can understand that the voltage across the capacitor increases in a linear fashion. This voltage is seen across the output and looks like a ramp waveform. This prevents the output from changing abruptly when the input changes and the output slew rate is determined by the capacitance of the compensation capacitor and the driving current. This basic principle is used to compensate for almost all op-amps.
As we now understand what is slew rate and why they are part of an opamp, to get more details check my original article how to measure and calculate the slew rate.